3. 확장 - K번째 큰 값
핵심 아이디어: 삽입정렬
첫번째 방법인 정렬의 경우 이 문제를 구현하는 것은 매우 쉽다. 원 코드에서는 반환값에서 두 번째를 의미하는 1을 인덱스로 했는데 그 대신 새로 받은 K-1번째 값을 반환하면 된다. 코드는 대략 이렇게 된다.
def kth_largest_number(arr, K):
unique_nums = set(arr)
sorted_nums = sorted(unique_nums, reverse=True)
return sorted_nums[K-1]함수의 이름의 접두사를 second 가 아닌 K번째를 의미하는 kth 로 변경했다. 그리고 사용자가 원하는 순서를 뜻하는 K 인자를 받는다. 코드는 두 번째 큰 값을 찾던 원래 코드와 거의 일치하며, 반환할 때만 인덱스를 K-1 로 하면 된다.
정렬의 경우는 쉬웠는데 두 번째 알고리즘은 까다롭다. 가령 K가 100이라고 해보자. 어떻게 100번째 값을 저장해야 하는가. 원 코드를 참조해 첫 번째, 두 번째, 세 번째, …, 100번째 큰 값을 담는 100개의 변수를 설정해야 할까?
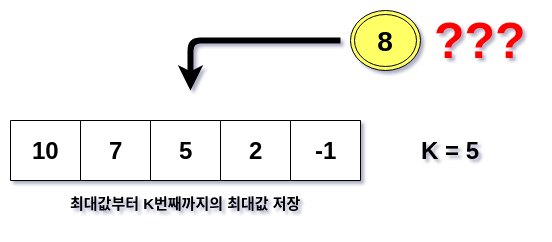
이 경우에는 배열에 최대값부터 K번째까지의 값을 저장하는 것이 바람직해보인다. 애초에 그럴 용도로 배열을 쓰는거니까. 이 방법이 K개의 줄에 변수 할당식을 쓰는 방법보다 훨신 유용해보인다. 이 포스트에서는 이 용도의 배열을 memory라고 표현하겠다.
그 다음으로, 반복문의 한 번의 순회에서 어떻게 if 문을 써나가야 할까? 아까 K가 2개인 경우에 우리가 상정해야 할 케이스가 3가지였다. 그러면 K에 대해서는 K+1 가지의 케이스를 고려해야 한다는 것인데.
이 경우에도 memory를 반복문으로 순회하며 새로운 값을 뒤집어써야 할 경우에 값을 재설정하면 될 것 같다.
마지막으로 하나 더 고려해야 한다. 원 배열을 순회할 때 K개의 값을 갖는 memory에 첫 번째부터 K번째 큰 값까지 유지·변경할텐데 이 과정을 어떻게 해야 할까? 가령 K가 5고 배열 순회 중 세 번째 큰 값보다 큰 새로운 값을 찾았을 때 어떻게 이를 기록할까?
힌트는 아까 만든 두 번째 큰 값을 찾는 코드의 비교 부분을 보면 된다.
for n in arr:
if n > largest:
second = largest
largest = n정확히 필요한 부분만 가져왔다. 만약 지금 순회하는 배열의 값 n 이 가장 큰 값(largest)보다 클 경우 largest 를 바로 n 으로 할당하는 것이 아니라, 두 번째 값을 *largest* 으로 재설정한 뒤, *largest* 값을 *n* 으로 뒀다.
이것을 현재 문제로 확장하면 현재 배열의 값(*n*)보다 작은 값을 찾으면 그 뒤의 원소들을 모두 한 번씩 뒤로 물린 뒤에 그 위치에 *n* 을 두는 것이 핵심이다.

이는 흡사 삽입정렬(insertion sort)을 연상시킨다. 삽입정렬에서도 오름차순일 때 현재 값보다 작은 값을 찾으면 뒤의 나머지 값을 모두 하나씩 뒤로 미룬 뒤에 값을 할당했으니까. 이제 이 핵심개념을 토대로 실제 코드를 작성해보자.
실제 코드
def kth_biggest(arr, K):
"""숫자 배열에서 K번째로 큰 값을 구한다.
이 함수는 고유한 값을 대상으로 한다.
가령 [2, 2, 1]에서 2번째로 큰 값은 2가 아닌 1이다.
또한 K가 배열의 고유한 값들의 개수보다 크면 IndexError를 반환한다.
:input:
arr | list := 숫자 배열
K | int := 1 이상의 정수를 대상으로 한다.
:return:
int := 배열에서 K번째로 큰 값
"""
# 예외 처리: K는 배열의 고유한 값 개수보다 클 수 없다.
ORDINAL_MSG = ('st', 'nd', 'rd')[K-1] if K <= 3 else 'th'
unique_set = set(arr)
if len(unique_set) < K:
raise IndexError(f"There's no {K}{ORDINAL_MSG} value in array")
elif K <= 0 or not arr:
raise ValueError("K should be over 0 and arr should not be empty")
# 상수 및 변수 선언
INF = float('inf')
memory = [-INF] * K
# 실제 검색 연산
for n in arr:
if n <= memory[-1]:
continue
for i, m in enumerate(memory):
if (i == 0 and n > m) or m < n < memory[i-1]:
for j in range(len(memory)-2, i-1, -1):
memory[j+1] = memory[j]
memory[i] = n
break
return memory[-1]실제 코드를 만들었다. 이 부분이 이 포스트에서 제일 중요해서 docstring과 에러체크하는 부분까지 다 넣어 완전한 기능으로 완성했는데 중요한 각 부분을 확인하면 다음과 같다.
# 예외 처리: K는 배열의 고유한 값 개수보다 클 수 없다.
ORDINAL_MSG = ('st', 'nd', 'rd')[K-1] if K <= 3 else 'th'
unique_set = set(arr)
if len(unique_set) < K:
raise IndexError(f"There's no {K}{ORDINAL_MSG} value in array")
elif K <= 0 or not arr:
raise ValueError("K should be over 0 and arr should not be empty")실제 코드를 작성하기 전에 arr, K 가 올바른 값인지 확인하는 과정을 거쳤다. 정상적으로 기능이 작동하기 위해서는 arr 은 비어있으면 안 되고, K 는 1 이상의 정수여야 하며, arr 의 고유한 값의 개수(데이터베이스 용어로는 ‘cardinality’)보다 커서는 안 된다. 이 조건을 검증했다.
주석 바로 위의 줄은 개인적인 욕심으로 적었는데 고유한 값의 개수가 K 보다 작을 경우 “There’s no 1st value..” 와 같은 메시지를 넣고 싶었다. 그런데 서수 표현에서 숫자에 따라 뒤에 붙는 기호가 ‘st’, ‘nd’, ‘rd’, ‘th’와 같이 변하기 때문에 이를 위한 코드를 넣었다.
# 상수 및 변수 선언
INF = float('inf')
memory = [-INF] * K첫 번째부터 K번째 큰 값까지 저장할 memory 를 선언했다. 크기는 당연히 K 인데, 각 값을 음의 무한대로 초기화한 것을 눈여겨볼만하다. 여기에는 최대값 이하 숫자들이 들어갈 것이기 때문에 가급적 최소값으로 해놓으면 무리없이 각 원소가 채워질 것이다.
for n in arr:
if n <= memory[-1]:
continue배열의 원소마다 순회한다. 각 숫자로 실질적인 알고리즘을 진행하기 전에 먼저 이 숫자와 현재 memory 의 K번째 값과의 대소관계를 비교한다. 이 이유는 현재 n 이 지금까지의 memory의 최소값보다 작거나 같으면 밑에 중첩된 반복문 자체를 실행하지 않아도 되기 때문이다. 따라서 이 경우에는 continue 로 건너 뛴다. 이제 핵심 부분으로 넘어가자.
for n in arr:
for i, m in enumerate(memory):
if (i == 0 and n > m) or m < n < memory[i-1]:
for j in range(len(memory)-2, i-1, -1):
memory[j+1] = memory[j]
memory[i] = n
break
return memory[-1]n 과 memory의 각 값을 비교하기 위해 for 문을 중첩했다. 이때 n 과 현재 비교하는 memory 의 값을 m 이라고 할 때, n 이 memory 에 들어오기 위해서는 n\ 은 *m* 보다 커야하고 *m* 의 바로 앞의 값보다는 작아야 한다. 그 검증을 if 문에서 하고 있다. 단, m 이 첫 번째 원소라면 m 의 바로 앞의 값은 없기 때문에 i가 0일 때는 따로 검증해 or로 묶는다. 이렇게 하지 않으면 memory[i-1] 부분에서 ‘-1’이라는 엉뚱한 인덱스가 튀어나올 수 있다.
만약 조건식에서 True가 반환된다면, 다시 말해 n 이 값을 뒤집어써야 할 m 과 그 위치를 찾았다면 다시 한 번 반복문을 실행한다. 값을 하나씩 뒤로 밀어야하기 때문이다. 이때 현재 m 의 위치 i 가 아니라 맨 뒤에서부터 거꾸로 앞의 값을 현재 위치로 뒤집어써야 한다는 것을 명심하자. 두 번째 큰 값을 찾는 코드에서도 n 이 largest 보다 클 때 largest 보다 second 변수가 먼저 재설정됐다는 것을 보면 납득할 수 있다.
현재 m 의 위치 i 의 바로 뒤까지 값이 밀렸으면 이제 i 에 n 을 할당한다. 그러면 현재까지의 최대값이 경신된다.
반복문을 완전히 탈출한 뒤에 memory의 마지막 값이 K번째 최대값이기 때문에 이를 반환하면 된다.
출처:https://shoark7.github.io/programming/algorithm/second-largest-number-in-array
'Python > Algorithm' 카테고리의 다른 글
| 문자열 - 다이얼 (0) | 2020.03.12 |
|---|---|
| 정수를 자릿수별로 쪼개기 (0) | 2020.03.12 |
| 한수 (0) | 2020.03.12 |
| Self number 셀프 넘버 (0) | 2020.03.12 |
| 숫자 배열에서 두 번째로 큰 값 찾기 (0) | 2020.03.10 |
